中学受験指導専門プロ家庭教師の普連土学園中学校過去問研究
普連土学園中学校受験指導はスペースＯＮＥのプロ家庭教師にお任せください。
 |
ご依頼専用ダイヤル |
0120-604-405 |
| お問い合わせ(東京本部) |
03-6868-6040 |
 |
お問い合わせメール
|
|
 |
ws-spaceone |
|
プロ家庭教師集団スペースONE
中学受験案内HOME
普連土学園中学校高等学校入試問題(過去問)解答解説
普連土学園中学校高等学校算数過去問研究
2018年度普連土学園中学校第3回入試問題から 今回は[3]の整数の性質を解説します。(1)は等差数列の和を用いて計算します。(2)は6の約数で考えましょう。
3..整数の性質にチャレンジ 問題
スペースＯＮＥのプロ家庭教師の解答で、普連土学園中学校の発表ではありません。
（1）解説解答
| (1) すべて足し合わせるといくつになりますか。 |
| 解説 |
| 等差数列の和 より |
 |
|
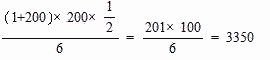| 答え 3350 |
|
|
（2）解説解答
| (2) 約分できる分数をすべて除いたとき、残った分数の合計はいくつになりますか。 |
| 解説 |
6の約数は(1，2，3，6)なので、
1から200までの2の倍数の個数は 200÷2 = 100個
よって 2の倍数の和は (2 + 200)×100÷2 = 10100
同様に 3の倍数の個数は 200÷3 = 66・・・2
3の倍数の和は (3 + 200 - 2)×66÷2 = 6633
6の倍数の個数は 200÷6 = 33・・・2
6の倍数の和は (6 + 200 - 2)×33÷2 = 3366
したがって 約分できるできる分数の和は
|
 |
|
|
ＨＯＭＥ
このホームページのすべての文章の文責および著作権はプロ家庭教師集団スペース ONEに属します。
普連土学園中学校・高等学校過去問研究TOPに戻る