| ���˗���p�_�C���� | 0120-604-405 | |
| ���₢���킹(�����{��) | 03-6868-6040 | |
| ���₢���킹(�����Z) | 093-592-6658 | |
���₢���킹���[�� |
||
| ws-spaceone |
���w�w�����v���ƒ닳�t�̌c���`�m�������ߋ��⌤��
�c���`�m�������w���̓X�y�[�X�n�m�d�̃v���ƒ닳�t�ɂ��C�����������B
| ���˗���p�_�C���� | 0120-604-405 | |
| ���₢���킹(�����{��) | 03-6868-6040 | |
| ���₢���킹(�����Z) | 093-592-6658 | |
���₢���킹���[�� |
||
| ws-spaceone |
2012�N�x�c���`�m�������Z���������́@��N�ʂ�̖��\���ŁA���̏o��̕�����l�ł����B�P�D�Q�D�R���v�Z�Q����܂ޏ���W���v�P2��@�S�D���ʐ}�`��̓]�ړ��@�T�D�U�D�L���@�V�D���̐}�`�@���o�肳��܂����B��s���͓���Z�S���삩�疞�ՂȂ��o�肳��Ă��܂��B
�͓r������K�v�Ƃ��Ȃ����ɐ����݂̂��������ތ`���ł����B
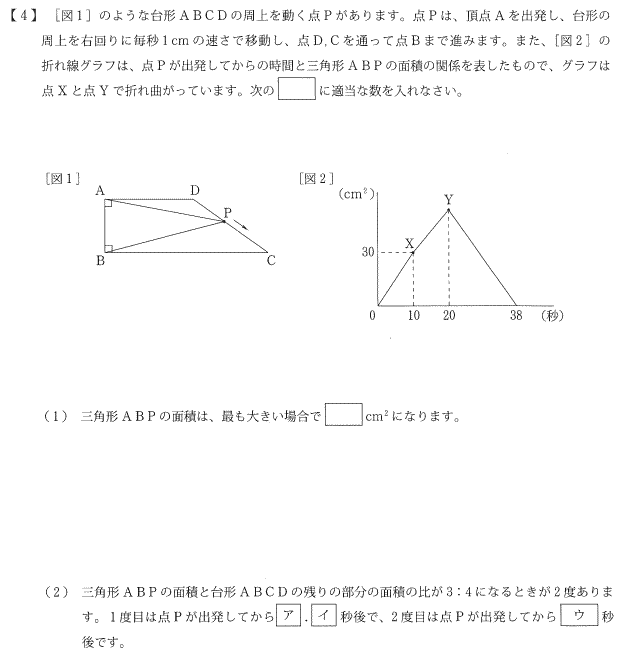
����́@�c���`�m�������Z���������p�o�̂S�D�}�`��̓_�ړ�����������܂��B
�Z���������@���ʏ�̓_�ړ��Ƀ`�������W
 |
||||
|
|||||||||||
|
���̃z�[���y�[�W�̂��ׂĂ̕��͂̕��ӂ���ђ��쌠�̓v���ƒ닳�t�W�c�X�y�[�X ONE�ɑ����܂��B