[PR] この広告は3ヶ月以上更新がないため表示されています。
ホームページを更新後24時間以内に表示されなくなります。

	ご依頼専用ダイヤル	0120-604-405
	お問い合わせ(東京本部)	03-6868-6040
	お問い合わせ(福岡校)	093-592-6658

	お問い合わせメール
	skype：ws-spaceone

プロ家庭教師集団スペースONE

中学受験案内HOME

入会案内へ

2011年度攻玉社中学校一般学級入試問題(過去問)解説

攻玉社中学校一般学級過去問研究

2011年度攻玉社中学校一般学級算数第１回入試問題は　１．四則計算3問を含む小問４問　２．規則性（暦と割合）　３．旅人算グラフ（動く歩道）　４．平面図形　相似形　５．立体図形　の大問５題構成で、出題内容・問題構成ともに例年通りでした。

2011年度第１回一般学級算数受験者平均点は45.2点　合格者平均点は59.5点。　

昨年度より算数・国語共に大幅に問題が難化し、昨年４科合計合格最低点186点が　2011年度は170点と低い結果になりました。

今回は　4．相似形を解説します。

算数入試問題（平面図形；相似形にチャレンジ）

４　問題

スペースＯＮＥプロ家庭教師の解説・解答で攻玉社中学校の発表ではありません。

（１）解説解答

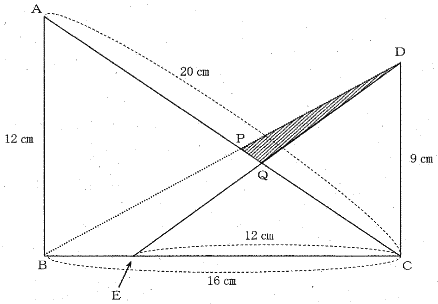
辺ＤＥの長さを求めなさい。

解説

直角三角形ＡＢＣと直角三角形ＤＣＥは相似形なので、、辺の比（相似比）は１２：９＝４：３

よって　ＡＣ：ＤＥ＝４：３　　　ＡＣ＝２０ｃｍなので、　　ＤＥ＝２０÷４×３＝１５

答　　　　１５ｃｍ

（２）解説解答

(2)　三角形ＱＥＣについて、次のものを求めなさい。
①　周囲の長さを求めなさい。
②　面積

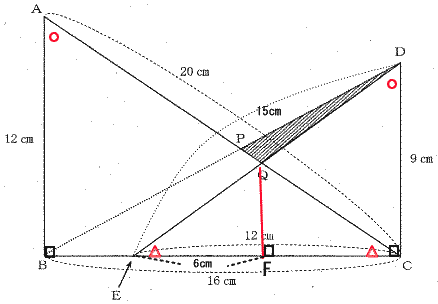
①　解説
直角三角形ＡＢＣと直角三角形ＤＣＥは相似形なので、対応する角度はそれぞれ等しいから、等しい角度は図の通り。よって三角形ＱＥＣは二等辺三角形なので、辺ＱＥ＝辺ＱＣ点Ｑから辺ＥＣに垂線をおろし、その交点をＦとする。三角形ＱＥＦと三角形ＤＥＣは相似形である。ＥＦ：ＥＣ＝６：１２＝１：２　なので、相似比は１：２。 (1)より　ＤＥ＝１５ｃｍ　なので、　ＥＱ＝ＣＱ＝１５÷２＝７．５ｃｍ三角形ＱＥＣの周囲の長さは　ＥＱ＋ＣＱ＋ＥＣ＝１５＋１２＝２７ｃｍ

②　解説
①よりＥＱ：ＱＤ＝１：１よって　三角形ＥＱＣ：三角形ＱＣＤ＝１：１　なので　三角形ＥＱＣの面積は三角形ＥＣＤの面積の1/2. 三角形ＥQＣの面積は　１２×９÷２÷２＝２７ｃ㎡

答　　①　　２７ｃｍ　　　　②　　２７ｃ㎡

（３）解説解答

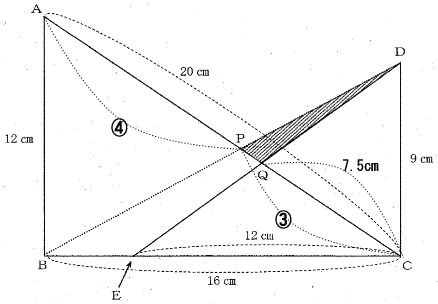
AP ： PQ ： QCを求めなさい。
解説
(2)①より　CQ＝７．５ｃｍ三角形ABPと三角形CDPは相似形。 AB：CD＝１２：９＝４：３なので、PA：CP＝４：３　　よって APの長さは　２０÷７×４＝80/7 CPの長さは　２０÷（３＋４）÷３＝60/7 AP : CQ : QP = 80/7 : 60/7 - 7.5 : 7.5 = 32:3:21
答　　　３２：３：２１

（４）解説解答

三角形DPQの面積を求めなさい。
解説
（３）より　QP：CQ＝３：２１＝１：７　なので三角形DPQ：三角形DQC＝１：７（２）②から　三角形DQC＝三角形EQCの面積は２７ｃ㎡よって三角形DPQの面積は　２７÷７＝27/7ｃ㎡
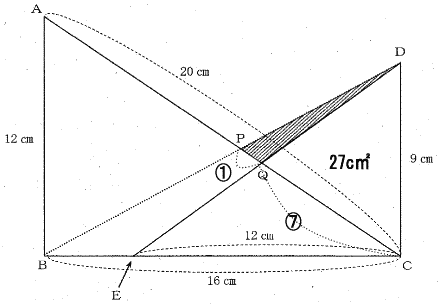答　　　27/7 ｃ㎡