 |
|
‚P•س1cm‚جƒ}ƒX–ع‚إ‚إ‚«‚½•\‚ھ‚ ‚è‚ـ‚·پB‚QŒآ‚جƒTƒCƒRƒچ‚ً‚S‰ٌگU‚é‚ئ‚«, ژں‚جƒ‹پ[ƒ‹‚إƒ}ƒX–ع‚ًˆح‚ف‚ـ‚·پB
ƒ‹پ[ƒ‹
‡@‚QŒآ‚جƒTƒCƒRƒچ‚ًگU‚è, ڈo‚½–ع‚جگ”‚جچ‡Œv‚ًƒ|ƒCƒ“ƒg‚ئ‚µ‚ـ‚·پB
پi—لپF‚P‚ئ‚T‚ج–ع‚ھڈo‚½‚ç, ‚Uƒ|ƒCƒ“ƒgپj
‡A‚QŒآ‚ئ‚à“¯‚¶–ع‚ھڈo‚½‚ئ‚«‚ح, ڈo‚½–ع‚ًچ‡Œv‚¹‚¸‚ة, –ع‚جگ”‚ًƒ|ƒCƒ“ƒg‚ئ‚µ‚ـ‚·پB
پi—لپF‚S‚ئ‚S‚ج–ع‚ھڈo‚½‚ç, ‚Sƒ|ƒCƒ“ƒgپj
‡B•\‚ح‰،‚ةƒTƒCƒRƒچ‚ًگU‚ء‚½‰ٌگ”, ڈc‚ًƒ|ƒCƒ“ƒg‚ئ‚µ‚ـ‚·پB
‡C•\‚جڈc‚ج‚Pƒ}ƒX‚ح‚Qƒ|ƒCƒ“ƒg‚ً•\‚µ‚ـ‚·پB‚Qƒ|ƒCƒ“ƒg‚إ‚Pƒ}ƒX‚ًˆح‚ف,
‚Pƒ|ƒCƒ“ƒg‚إ‚ح‚Pƒ}ƒX‚ج”¼•ھ‚ًژخ‚ك‚ةˆح‚ف‚ـ‚·پB
‚µ‚½‚ھ‚ء‚ؤ, ‚Rƒ|ƒCƒ“ƒg‚إ‚ح, ‚Pƒ}ƒX‚ئ”¼•ھ‚ًˆح‚ف‚ـ‚·پB
‡Dƒ}ƒX–ع‚ًˆح‚ق‚ئ‚«, ˆح‚ء‚ؤ‚إ‚«‚鑽ٹpŒ`‚جٹpگ”‚ھچإ‚àڈ¬‚³‚‚ب‚é‚و‚¤‚ةˆح‚ف‚ـ‚·پB |
|
|
|
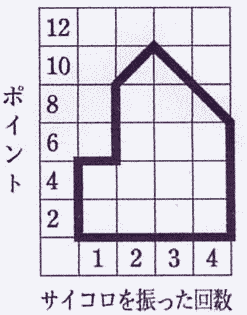
—لپF‚P‰ٌ–ع‚جƒTƒCƒRƒچ‚جڈo‚½–ع‚جچ‡Œv‚ھ‚S,
‚Q‰ٌ–ع‚جƒTƒCƒRƒچ‚جڈo‚½–ع‚جچ‡Œv‚ھ‚X,
‚R‰ٌ–ع‚جƒTƒCƒRƒچ‚جڈo‚½–ع‚جچ‡Œv‚ھ‚X,
‚S‰ٌ–ع‚جƒTƒCƒRƒچ‚جڈo‚½–ع‚جچ‡Œv‚ھ‚V‚ج‚ئ‚«, ‰E•\‚ج‚و‚¤‚ةƒ}ƒX–ع‚ھˆح‚ـ‚ê‚ـ‚·پB
|
 |
|
|
‚±‚ج‚ئ‚«, ژں‚ج–â‚¢‚ة“ڑ‚¦‚ب‚³‚¢پB
(‚P) —ل‚ج•\‚جˆح‚ـ‚ꂽ•”•ھ‚ج–تگد‚ً‹پ‚ك‚ب‚³‚¢پB
(‚Q) ˆح‚ـ‚ꂽ–تگد‚ھچإ‚à‘ه‚«‚‚ب‚é‚ئ‚«, ‚»‚ج–تگد‚ً‹پ‚ك‚ب‚³‚¢پB
(‚R) ˆح‚ـ‚ꂽگ}Œ`‚ھ’¼ٹp“ٌ“™•سژOٹpŒ`‚ئ‚ب‚éڈêچ‡‚إ, ƒ|ƒCƒ“ƒg‚جچ‡Œv‚ھچإ‚àڈ¬‚³‚‚ب‚é‚ئ‚«‚ئ, چإ‚à‘ه‚«‚‚ب‚é‚ئ‚«‚ج’l‚ً, ‚»‚ꂼ‚ê‹پ‚ك‚ب‚³‚¢پB |
|
|
|
|
|
|
|
|
 |
 |