プロ家庭教師集団スペースONE

中学受験案内HOME

2010年度栄東中学校東大クラス選抜入試問題(過去問)解答解説

栄東中学校算数過去問研究

2010年度栄東中学校東大クラス選抜算数入試問題は　１．小問集合４問　２．規則性（場合の数）　３．平面図形（速さ）　４．立体図形　大問４題構成でした。

算数入試問題（平面図形と速さにチャレンジ）

下の図のように、半径６ｃｍ，４ｃｍ，２ｃｍの半円を３つ組み合わせて出来た図形があり、半径６ｃｍの円の中心をＯ，その直径の両端をＡ，Ｂとします。

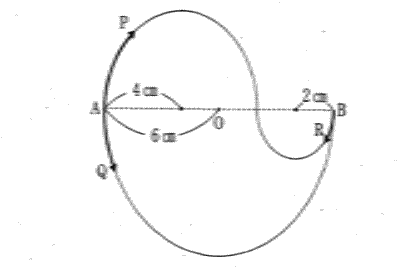点Ｐ，Ｑは点Ａを，点Ｒは点Ｂをそれぞれ同時に出発し、矢印の方向に一定の速さで動きます。点Ｐは半径１ｃｍの円周上をちょうど１周するのに１秒かかる速さで動き、点Ｑは点Ｐの1/2倍の速さで、点Ｒは点Ｐの2/7倍の速さで動きます。このとき、次の問にそれぞれ答えなさい。

（１）　点Ｐと点Ｒが初めて出会うのは、出発してから何秒後ですか。

（２）　点Ｐと点Ｒが初めて出会う点をＤ，そのときの点Ｑの一をＥとするとき、角ＤＯＥの大きさを求めなさい。

スペースＯＮＥのプロ家庭教師の解答で、栄東中学校の発表ではありません。

（１）解説解答　

点Ｐと点Ｒが初めて出会うのは、出発してから何秒後ですか。
解説
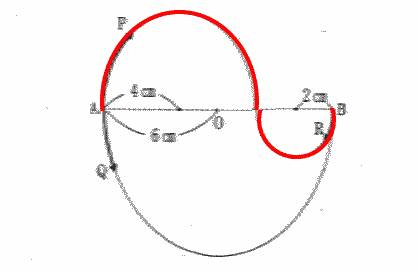
計算しすぎない計算の工夫を考えましょう。点Ｐの速さは　１秒間で半径１ｃｍの円周上をちょうど１周するので　　１×２×３．１４＝２×３．１４ｃｍ/秒点Ｒの速さは、点Ｐの2/7倍の速さなので　　　２×３．１４×2/7＝4/7×３．１４点Ｐと点Ｒ同時に出発するときの間の距離は　右図の赤線部分なので　　８×３．１４÷２＋４×３．１４÷２＝（４＋２）×３．１４＝６×３．１４よって　点Ｐと点Ｒが初めて出会うのは６×３．１４÷（２×３．１４＋4/7×３．１４）＝６×３．１４÷18/7÷３．１４＝７/３
答　　７/３秒後

点Ｐと点Ｒが初めて出会う点をＤ，そのときの点Ｑの一をＥとするとき、角ＤＯＥの大きさを求めなさい。
解説
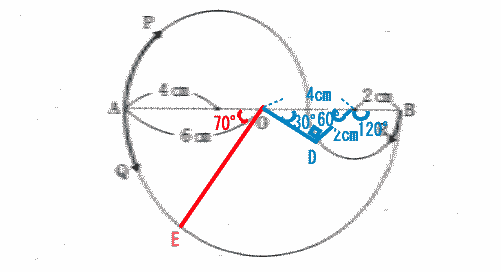
(1)より　点Ｐと点Ｒが初めて出会うのは　出発して７/３秒後なのでＤ：点Ｒが秒速　（4/7×３．１４）ｃｍで７/３秒進んだ地点　4/7×３．１４×７/３＝4/3×３.１４　4/3×3.14÷（４×3.14）＝1/3 　1/3×３６０＝１２０°　・・・半径２ｃｍの半円を１２０°進んだ地点Ｅ：点Ｑが　Ａ点よりＰと反対方向に秒速３.１４ｃｍで7/3秒進んだ地点　３.１４×7/3ｃｍ　３.１４×7/3÷（１２×３.１４）＝7/36 　7/36×３６０＝７０°・・・半径６ｃｍの半円を７０°進んだ地点右図のように　点Ｏ点Ｄと半径２ｃｍの中心とを結んで出来る三角形は　２辺の長さの比が　２ｃｍ：４ｃｍ＝１：２６０°９０°の直角三角形になるので角ＤＯＥ＝１８０ー（７０＋３０）＝８０
答　　　８０°

栄東中学校受験　傾向と対策に戻る

中学受験過去問研究ＴＯＰ

プロ家庭教師集団スペースＯＮＥリンク集

高校受験数学・英語過去問研究

大学受験過去問研究

医学部受験過去問研究

医科大学・医学部入試情報

ＨＯＭＥ