中学受験指導専門プロ家庭教師の芝中学校過去問研究
芝中学校受験指導はスペースＯＮＥのプロ家庭教師にお任せください。
 |
ご依頼専用ダイヤル |
0120-604-405 |
| お問い合わせ |
03-6868-6040 |
 |
お問い合わせメール
|
|
 |
ws-spaceone |
|
プロ家庭教師集団スペースONE
中学受験案内HOME
入会案内へ
芝中学校入試問題(過去問)解答解説
芝中学・高等学校2014年度算数過去問研究
2014年度芝中学校第１回算数入試問題は 例年通りの出題構成で １．計算２問 ２．～１０． 一行問題・大問の組み合わせでした。
解答形式も例年通り 答のみを解答欄に書く形式でした。
2014年度第１回の算数最高点 94点 合格者平均69.3点 受験者平均は52.0点 でした。
プロ家庭教師集団スペースＯＮＥの解説・解答で芝中学校の発表ではありません。
(1) 解説解答
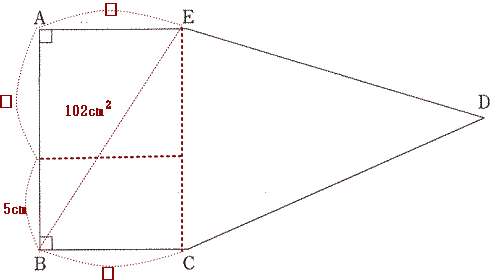
| (1) 点Pは点Aを出発して□秒後に点Cに到着します。 |
|
| 解説 |
|
グラフより 点Pが辺BC上を移動する間、三角形APEの面積は102c㎡
よって 長方形ABCEの面積は204c㎡
AE = BC = □ｃｍとすると、AB = (□ + 5)cm
長方形ABCEの面積は □×(□ + 5) = □×□ + □×5 = 204
10×10 = 100 より □に11から適する数字を探すまで当てはめていくと、
12×12 + 12×5 = 204
したがって、AB = BC = 12cm, AB = 12 + 5 = 17cm
点Pが点Aを出発して、点Cに到着するまでに動く距離は 17 + 12 = 29cm
点Pの速さは秒速1cmなので、点Cに到着するのは 29秒後 |
 |
|
|
| 答 29秒後 |
|
|
|
(2) 解説解答
| (2) 点Pが点Aを出発してから20秒後の三角形APEの面積が、51.1秒後の三角形APEの面積の２倍であるとき、DEの長さは□cmです。 |
| 解説 |
|
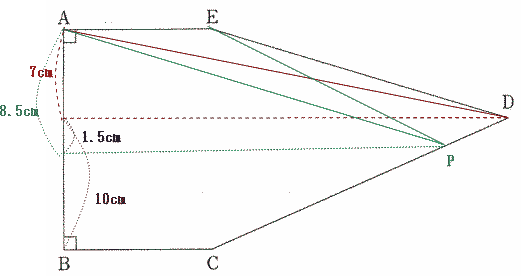
グラフより点Pが点Dに到着したときの三角形APEの面積は42c㎡，AEを底辺としたときの三角形の高さは 42×2÷12 = 7cm。
また点Pが点Aを出発してから20秒後は点Pがは辺BC上にあり、点Cを通過して 51.1 - 29 = 22.1秒後の三角形APEの面積の２倍であるので、点Pが辺BC上にあるときと、51.1秒後の高さの比は2：1より、51.1秒後のAEを底辺としたときの三角形の高さは 17÷2
= 8.5cm。
|
 |
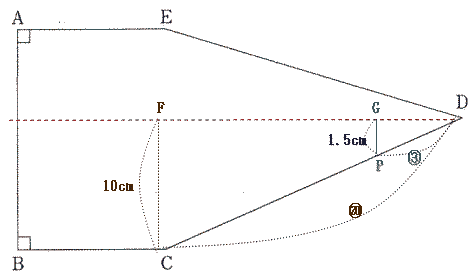
点Dから辺ABに垂線をおろし、また、その直線に点C，51.1秒後の点Pの位置から垂線をおろし、その交点をそれぞれ点F，点Gとすると、図の通り
三角形DGPと三角形DFCは相似形、相似比は1.5：10 = 3：20
⑳ - ③ = ⑰ = 51.1 - 29 = 22.1cm
したがって CDの長さ⑳は
22.1÷17×20 = 26cm
点Pが点Aを出発して点Dに到着するのに進む距離は 29 + 26 = 55cm
グラフより 点Pが点Eに到着するのは出発後80秒なので、80cm
よって DEの長さは 80 - 55 = 25cm |
 |
|
|
| 答 25cm |
|
|
|
ＨＯＭＥ
このホームページのすべての文章の文責および著作権はプロ家庭教師集団スペース ONEに属します。
芝中学校・高等学校受験 入試問題傾向と対策（過去問研究）TOPへ
芝中学校過去問研究ＴＯＰに戻る