中学受験指導専門プロ家庭教師の青山学院中等部入試問題解説

青山学院中等部受験指導はスペースＯＮＥのプロ家庭教師にお任せください。

	ご依頼専用ダイヤル	0120-604-405
	お問い合わせ	03-6868-6040
	お問い合わせメール
	ws-spaceone

プロ家庭教師集団スペースONE

中学受験案内HOME

2011年度 青山学院中等部入試問題（過去問）解答解説

青山学院中等部過去問研究

2011年度青山学院中等部算数入試問題は　昨年度より計算が１問増え３問、小問も１問増え９問、　枝問１付きの問題は２題の構成になりました。総解答数も１８から16になりました。例年通り１問ごとのボリュームの軽い、小問中心の出題構成。例年通り途中式を必要としない答のみを解答欄に書き込む解答形式でした。

2011年度青山学院中等部入試結果は　募集人数　男女約140名、志願者　男子513名　女子641名　合格者　男子103名　女子92名　合格最低点　男子189点　女子203点でした。

算数入試問題　　小問にチャレンジ

問題

青山学院中等部過去問研究ＴＯＰに戻る

スペースＯＮＥプロ家庭教師の解答で、青山学院中等部の発表ではありません。

[4] 最小公倍数最大公約数　解説・解答

解説 14/75を整数にするには75の倍数をかけ、42/55を整数にするには55の倍数をかけるとよいので、75と55の最小公倍数は825 分数で最も小さくするには、14でも42でも割りきれる数にしなければならない。　よって　14と42の最大公約数は14 よって　条件に合う分数は　825/14 答　　　　825/14

[5] 割合　解説・解答

[6] 折り返しの角度　解説・解答

図のように、長方形の紙を横の長さの半分のところで折った折り目に2つの頂点を合わせておりました。 [あ]の角は□度です。 解説 図の通り （い）の角度は　360ー（90×2＋84）＝96 （う）の角度は　（180ー96）÷2＝42 （あ）＋（あ）＝　180-42＝138 （あ）の　角度　　138÷2＝69 答　　　　６９度

[7] 割合　解説・解答

1枚のピザを、先にＡとＢの２人がとり、さらに残りの1/4をＣがとりました。３人のとった量はＢはＡの半分、ＣはＢの2/3でした。残ったピザは全体のァ/ィです。 解説 ３人のとった量はＢはＡの半分なので　ＡとＢのとったピザの量の比は　Ａ：Ｂ＝２：１、 ＣはＢの2/3なので、　ＢとＣのとったピザの量の比は　Ｂ：Ｃ＝３：２ よって　Ａ：Ｂ：Ｃ＝�E：�B：�A Ｃが残りの1/4とったので、Ｃのとった量�Aが残りの1/4にあたるので、ＡとＢとＣがとった残りの量は　�E，残りの全体量は�G ＡとＢの２人がとった量が�E＋�B＝�H　なので、　ピザの全体量は　�H＋�G＝�P よって　　残ったピザは　全体の　6/17 答　　　　ア：６　　　イ：１７

[8] 旅人算　解説・解答

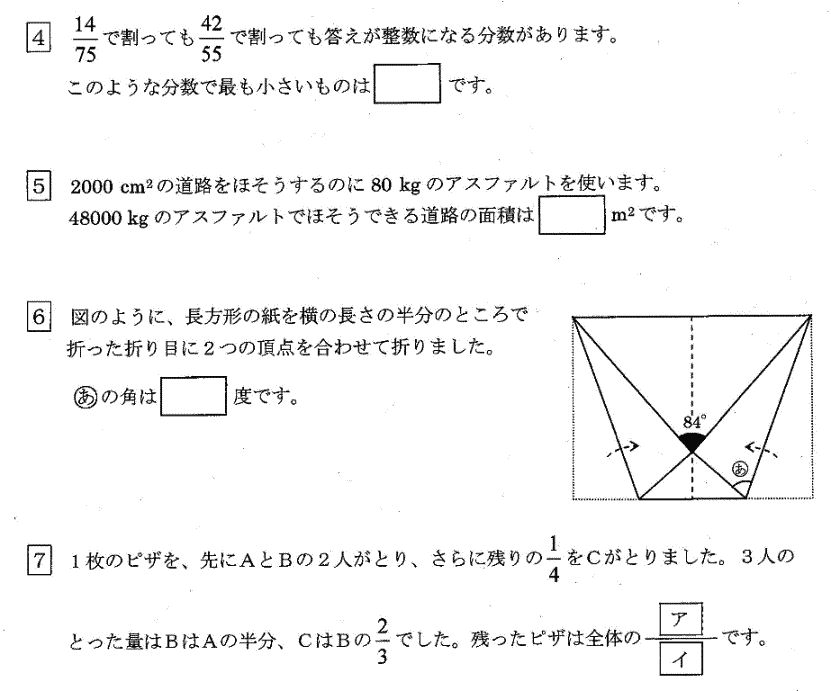
あき子さんと兄が家から同じ道をポストに向かってそれぞれ一定の速さで歩いています。８時にあき子さんはポストまで３５７ｍの地点にいて、兄の６３ｍ前方にいました。兄は８時３分にあき子さんを追い越し、８時５分にポストについて、すぐに同じ道を引き返しました。兄があき子さんと出会うのはポストから（　　　）ｍの地点です。 解説１ 兄は５分間で　（63＋357）ｍ進んだので、　兄の分速は　　（63＋357）÷５＝84m/分 兄は３分間であき子を追い越したので　　６３−３＝２１・・・・あき子と兄の速さの差 あき子の分速は　　８４−２１＝６３ｍ/分 兄が歩つとに着いたときふたりの間の距離は　３５７−６３×５＝４２ｍ ２人が再び出会うのは　　４２÷（８４＋６３）＝2/7分後 兄がポストから　2/7分歩いた地点　８４×2/7＝２４ 別解２ 解説１より　兄の分速は８４ｍ，あき子の分速は６３ｍ。 兄はポストを挟んで　あき子と反対側にいると置き換えると 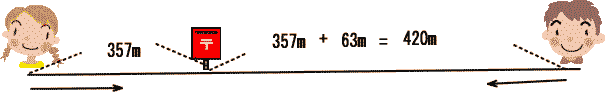兄とあき子の速さの比＝道のりの比は　８４：６３＝４：３ ふたりの間の距離　（４２０＋３５７）ｍを２人で同時に歩いて出会うのは　あき子が　（４２０＋３５７）×３／７＝３３３ｍ進んだ地点なので、 ポストから　３５７−３３３＝２４ｍの地点 答　　　　２４ｍ

[9] 平均算　解説・解答

よし子さんは１０回のテストの平均点の目標を立てました。９回目までの平均点は目標に３点足りませんでした。１０回目は９７点とりましたが、平均点は目標に１点足りませんでした。目標にしていた平均点は（　　　　　）点です。 解説 面積図で考えましょう。 図の通り　塗りつぶした部分の面積は等しいので ９×２＝１８ 平均点は　９７−１８＝７９点 目標点は　７９＋１＝８０点 天秤では �@＝２点なので、 �H＝２×９＝１８点 目標点は　　９７−１８＋１＝８０点 答　　　　８０点

[10] 割合　解説・解答

A,B,C,Dの４人でおはじきを使ったゲームをしました。 ゲームが終わって４人のおはじきの数を調べたところ、AとBの合計がCと同じで、AとDの合計がBと同じでした。 また、Cの２倍がDの３倍と同じで、Aは１２個でした。４人のおはじきの数の合計は（　　　　　）個です。 解説 Cの２倍がDの３倍と同じなので　　C×２＝D×３　　　C:D＝�B：�A AとBの合計がCと同じで、AとDの合計がBと同じなので、絵にすると �@＝１２×２＝２４ A：１２個，　　C＝�A：２４×２＝４８個，　　　D=�B：２４×３＝８４個，　　　B=A＋D：１２＋４８＝６０個 ４人のおはじきの数の合計は　　１２＋４８＋８４＋６０＝２０４個 答　　　２０４

青山学院中等部過去問研究ＴＯＰに戻る

青山学院中等部受験　傾向と対策に戻る

青山学院中等部受験過去問対策に戻る

プロ家庭教師集団スペースＯＮＥリンク集

高校受験過去問研究

大学受験過去問研究

医学部受験過去問研究

医科大学・医学部入試情報

ＨＯＭＥ

このホームページのすべての文章の文責および著作権はプロ家庭教師集団スペース ONEに属します。