中学受験指導専門プロ家庭教師の麻布中学校過去問研究

麻布中学校受験指導はスペースＯＮＥのプロ家庭教師にお任せください。

	ご依頼専用ダイヤル	0120-604-405
	お問い合わせ	03-6868-6040
	お問い合わせメール
	ws-spaceone

プロ家庭教師集団スペースONE

中学受験案内HOME

2008年度麻布中学校入試問題(過去問)解答解説

麻布中学校算数過去問研究　2008年度算数入試問題

算数入試問題　等積変形にチャレンジ

６問題

円の1/4の部分の図形OABがあります。次の問に答えなさい。
（１）下図において、斜線部分の面積と図形OABの面積の比を求めなさい。ただし、直線OA,CD,EFは平行です。

（２）　右の図のように図形ＯＡＢの弧ＡＢ（曲線の部分）を５等分した各点からＯＡに平行な直線を引きました。ＯＡを５等分したとき　２つの斜線部分の面積の和を求めなさい。

スペースＯＮＥ家庭教師の解答解説で麻布中学校の発表ではありません。

（１）解説　解答

下図において、斜線部分の面積と図形OABの面積の比を求めなさい。ただし、直線OA,CD,EFは平行です。
解説
９０－２５×２＝４０°　　９０－（２５＋４０）＝２５°　　９０ー２５＝２５＋４０＝６５°　　　　辺ＦＯ＝辺ＤＯ　・・・おうぎ形の半径　　三角形ＥＯＦと三角形ＣＯＤは合同の三角形　　　　　が共通の部分なので　　　は面積が同じよって　斜線部分の面積は扇形ＦＯＤの面積と等しい。　　斜線部分の面積と図形ＯＡＢの面積比は角度の比と等しくなる。　斜線部分の面積に等しい扇形の角度４０度　図形ＯＡＢの角度９０度　　４０：９０＝４：９
答　　　４：９

（２）解説　解答

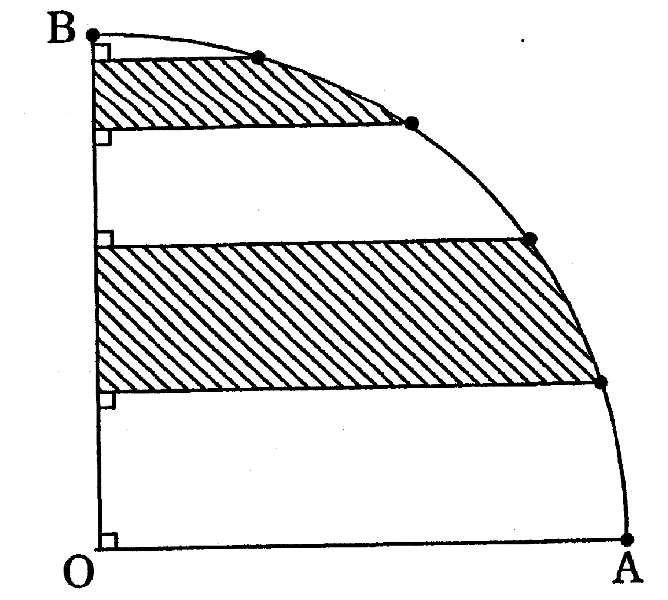
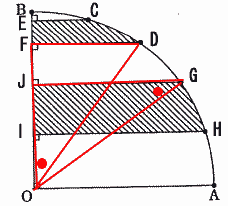
右の図のように図形ＯＡＢの弧ＡＢ（曲線の部分）を５等分した各点からＯＡに平行な直線を引きました。ＯＡを５等分したとき　２つの斜線部分の面積の和を求めなさい。
解説
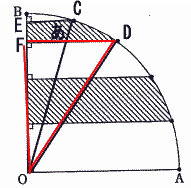
（あ）の面積弧CDと円の中心を結ぶおうぎ形の面積＋三角形ECO－三角形FDO ∠CODは図形OABを５等分しているので　９０÷５＝１８° よって　５×６×３．１４×18/360＋△ECO－△FDC
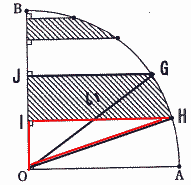
（い）の面積弧GHも中心角１８°なので中心角１８°のおうぎ形の面積＋三角形JGI－三角形IHO ∠CODは図形OABを５等分しているので　９０÷５＝１８° よって　５×６×３．１４×18/360＋△JGI－△IHO
また △ECOと△IHOは CO=HO(半径）,　∠CEO＝∠OIH＝９０°,　　∠ECO＝∠IOH＝９０－１８＝６２°なので合同,
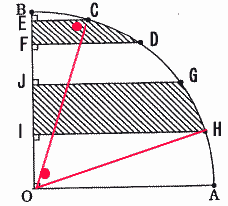△FDCと△JGIは DO＝GO（半径）,　　∠DFO＝∠OJG＝９０°,　　 ∠FDO＝９０÷５×２＝３６°,∠JGO＝９０－∠JOG＝９０－９０÷５×３＝３６°なので ∠FDO＝∠JGO よって　△FDCと△JGIも合同
２つの斜線部分の面積の和は５×５×３．１４×18/360＋△ECO－△FDC＋５×５×３．１４×18/360＋△JGI－△IHO ＝５×５×３．１４×18/360＋５×５×３．１４×18/360＋△ECO－△IHO＋△JGIー△FDC ＝５×５×３．１４×18/360＋５×５×３．１４×18/360＝５×５×３．１４×18/360×２＝７．８５

答　　　　７．８５ｃ㎡

麻布中学校過去問研究ＴＯＰに戻る

麻布中学校受験　傾向と対策に戻る

麻布中学校過去問対策へ

中学受験過去問研究ＴＯＰ

プロ家庭教師集団スペースＯＮＥリンク集

高校受験過去問研究

大学受験過去問研究

医学部受験過去問研究

医科大学・医学部入試情報

ＨＯＭＥ

このホームページのすべての文章の文責および著作権はプロ家庭教師集団スペース ONEに属します。