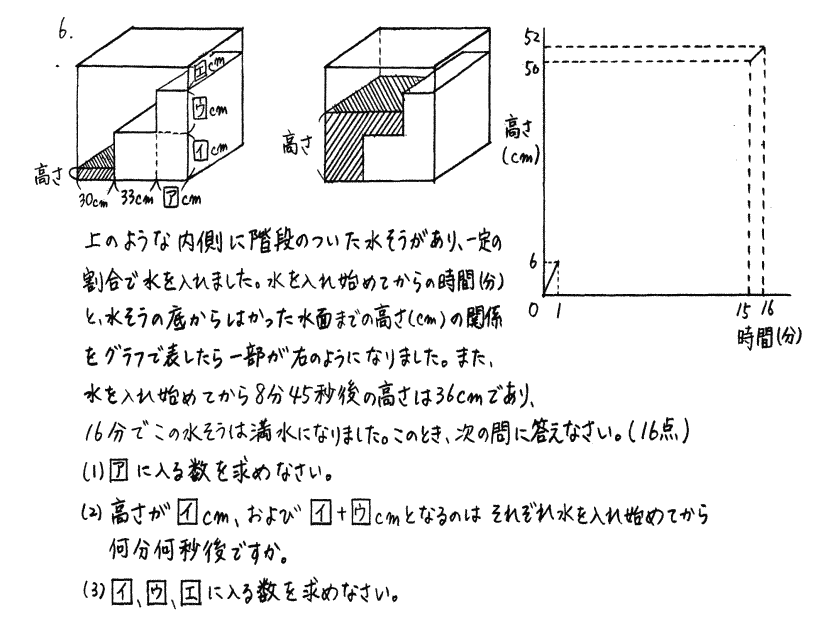
| (2) 高さが[イ]cm，および、[イ] + [ウ]cmとなるのは、それぞれ水を入れ始めてから何分何秒後ですか。 |
| (3) [イ]，[ウ]，[エ]に入る数を求めなさい。 |
| 解説解答 |
Aの部分は1分間に6cmずつ水面が上がるので、Aの部分のみを考えたとき、36cmまで水面が上がるのにかかる時間は 36÷6 = 6分間。よってBの部分は
8分45秒 - 6分 = 2分45秒で水が入る。A部分に入る水の底面積は 30×36 = 1080なので、6分間に入る水の量を1080とすると、1分間に入る水の量は 1080÷6
= 180
Bの部分に入る水の量は
横の長さが33cmなので、高さは 495÷33 = 15cm
よって[イ]の高さは 36 - 15 = 21cm
高さが[イ] = 21cmになるのは水を入れ始めてから 31×21÷180 = 3.5 = 3分30秒。
水面の高さが[イ] = 21cmから52cmになるまでにかかる時間は 16分 - 3分30秒 = 12分30秒
12分30秒間に入る水の量は 180×12.5 = 2250
鶴亀算の面積図より、
|
 |
[エ] = 11cm， [イ] + [ウ] = 52 - 11 = 41cm
[ウ] = 41 - 21 = 20cm
水面の高さが41cmになるのにかかる時間は 3分30秒 + (41 - 21)×63÷180 = 10.5 = 10分30秒 |
|
| 答 (2) 高さが[イ]cmになる時間 3分30秒，高さが[イ] + [ウ]cmとなる時間 10分30秒 |
| 答 [イ] 21cm，[ウ]20cm，[エ]11cm |
ラサール中学校過去問研究ＴＯＰに戻る
HOME
