���w�w�����v���ƒ닳�t�̗������w�@���w�Z�ē�
�������w�@���w�Z�w���̓X�y�[�X�n�m�d�̃v���ƒ닳�t�ɂ��C�����������B
 |
���˗���p�_�C���� |
0120-604-405 |
| ���₢���킹(�����{��) |
03-6868-6040 |
 |
���₢���킹���[��
|
|
 |
ws-spaceone |
|
�v���ƒ닳�t�W�c�X�y�[�XONE
 ���w�ē�HOME
���w�ē�HOME
����ē���
�������w�@���w�Z�������i�ߋ���j���
�������w�@���w�Z�ߋ��⌤��
20013�N�x�������w�@���w�Z�Z���������͗�N�ʂ�@�P�D�l���v�Z���܂ޏ���W��8��@�Q�D�ӎO�p�`�̉�]�}�`�@�R�D�L���@�S�D���ʏ�̓_�ړ��i�O���t�̓ǂݎ��j�̑��S��\���ł����B�����݂̂����ɏ������ތ`���ł����B
�����4��������܂��B
4�͕��ӂ�ǂݎ���Ďl�p�`�������ō�}���邱�Ƃɂ���ĉ�������ł��B
�X�y�[�X�n�m�d�v���ƒ닳�t�̉ŁA�������w�@���w�Z�̔��\�ł͂���܂���B
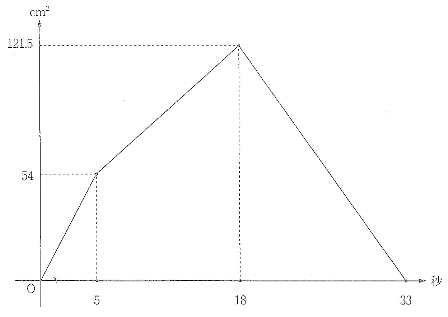
�O���t�̓ǂݎ��ƍ�}
|
 |
|
|
|
����1cm�Ȃ̂ŁA�O���t���AB�Ԃ̒�����5cm�CBC�Ԃ̒�����18 - 5 = 13cm�CCD�Ԃ̒�����33 - 18 = 15cm�BA�ɖ߂�̂�60�b������̂ŁADA�Ԃ̒�����
60-33 = 27cm�B |
|
|
|
�܂��@�_D��ʉ߂��A45�b��ɂ͒��p�O�p�`PCD�̖ʐς�54cm2�Ȃ̂ŁA45�b���DP�Ԃ̒����� 45 - 33 = 12cm�CPC�̒����́@54 = 12�~����2 ���@9cm�B
�_D��ʉ߂��A57�b��ɂ͒��p�O�p�`PAB�̖ʐς�6cm2�Ȃ̂ŁA57�b���PA�Ԃ̒����� 60 - 57 = 3cm�CPB�̒����́@6 = 3�~����2 ���@4cm.�B |
|
|
|
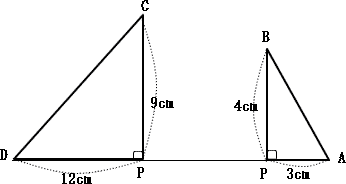
��DA��ɒ��p�O�p�`PCD�ƒ��p�O�p�`PAB����}����Ɓ@���}�̒ʂ� |
|
|
|
 |
|
|
|
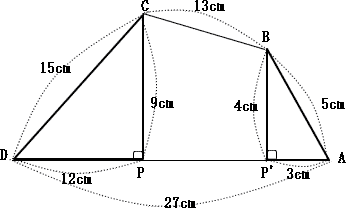
�_B�Ɠ_C���Ō��сA�o������57�b��̓_P��P'�Ƃ��āA��}������ƁA���̎l�p�`�͉��}�̒ʂ� |
|
|
|
 |
|
|
|
|
(1)����E��
| �l�p�`ABCD�̖ʐς͉�cm2�ł����B |
|
|
|
| ��� |
|
|
|
| �E�}�̒ʂ�A�l�p�`CPP'B�͑�`�B |
 |
|
|
����ċ��߂�ʐς͒��p�O�p�`PCD�̖ʐρ{��`CPP'B�{���p�O�p�`PAB�̖ʐρB
54 + (9 + 4)�~(27-12-3)��2 + 6cm = 138 |
|
|
|
|
|
|
| ���@�@138cm2 |
|
|
|
|
|
(2)����E��
| �_P���_A���o�����Ă���A23�b��̎O�p�`PAD�̖ʐς͉�cm2�ł����B |
|
|
|
| ��� |
|
|
|
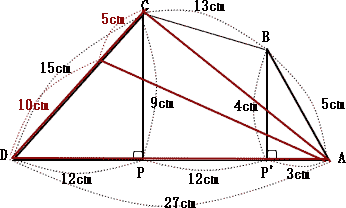
| 23 - 18 = 5�@����ā@�_C���߂���5�b��Ȃ̂Ł@���̂Ƃ���CP�̒����FPD�̒��� = 5�F15-5 = 5�F10 = 1�F2 |
 |
|
|
| �O�p�`ACD�̖ʐς́@27�~ 9 ��2 �@���̖ʐς��@�F�A�@�ɕ������Ƃ��̇A�̖ʐςȂ̂� |
|
|
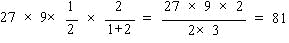 |
|
|
|
|
|
|
| ���@�@�@81cm2 |
|
|
|
|
|
(3)����E��
| �_�o���_�`���o�����Ă���A�O�p�`PAD�̖ʐς�54cm2�ƂȂ�̂�2��܂��B1��ڂ�5�b��ł��B2��ڂ͉��b��ł����B |
|
|
| ��� |
|
|
|
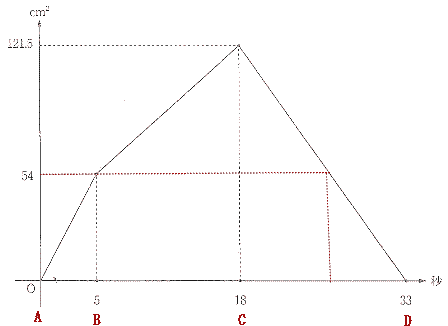
�O���t���_P���ӂb�c�Ԃ̂Ƃ��ɁA54cm2�ɂȂ�B
|
 |
|
|
�O�p�`ACD�̖ʐς́@27 �~9 ��2 = 121.5cm2
�O�p�`PAD�̖ʐς�54cm2�ƂȂ�Ƃ��A�O�p�`CAP�̖ʐς́@121.5 - 54 = 67.5cm2
����ā@�O�p�`CAP�̖ʐ� �F �O�p�`PAD = 67.5 �F 54 = 5�F4 ���
�@CD�Ԃ�_P��5 �F 4�ɕ�����ꍇ�̎��Ȃ̂ŁA
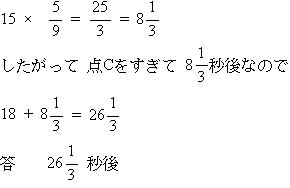 |
 |
|
|
|
|
�g�n�l�d
���̃z�[���y�[�W�̂��ׂĂ̕��͂̕��ӂ���ђ��쌠�̓v���ƒ닳�t�W�c�X�y�[�X ONE�ɑ����܂��B